Soy seguidor en Twitter de Eduardo Sáenz de Cabezón, @edusadeci, desde hace tiempo, a raíz de un monólogo científico muy simpático y ya muy conocido: "Las matemáticas son para siempre".
Por cierto, también tiene un canal en Youtube, llamado Derivando, que trata de temas matemáticos expuestos de forma simple y amena.
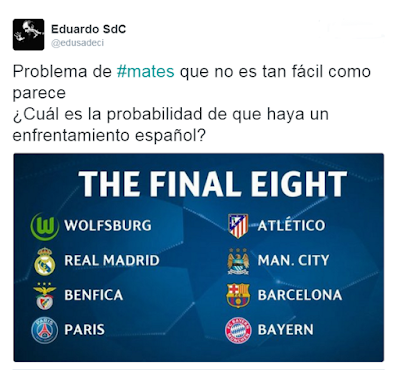
A veces lanza un "tuit-reto" matemático y, claro, como a mí también me gusta proponer alguno a mis alumnos, me siento aludido y, para ser consecuente y dar ejemplo, lo acepto. En este caso habla sobre la probabilidad de que haya un emparejamiento de equipos españoles en el sorteo de cuartos de final de la Liga de Campeones, conocida también por la Champions League. El tuit en cuestión era el siguiente:
Como no soy muy "futbolero", lo primero que tuve que hacer es enterarme de cómo se iba a realizar el sorteo. Parece ser que se trata de un sorteo abierto donde se extraen, de forma sucesiva y en una especie de ensaladera trasparente, bolas con forma de balón en cuyo interior se encuentra un papel con el nombre del equipo. Hay ocho bolas, cada una con el nombre de un equipo que ha llegado a cuartos de final, donde por cierto hay 3 equipos españoles (Real Madrid, Barcelona y Atlético de Madrid) y 5 no españoles (Wolfsburg, Benfica, Paris Saint-Germain, Manchester City y Bayern de Múnich). Las dos primeras bolas conforman el primer emparejamiento, las dos siguientes otro y así sucesivamente hasta obtener los cuatro emparejamientos. La información la he obtenido de la página web de la UEFA Champions League donde incluso se pueden ver los vídeos del sorteo.
Con la información completa, pasamos a la fase de pensar cómo se podría calcular la probabilidad pedida. Para no extenderme, tengo que confesar que, como dice Eduardo en el tuit, "no es tan fácil como parece": usé métodos que, aún siendo correctos en su planteamiento y permitiendo obtener una respuesta, no eran eficientes. Explico la no eficiencia: demasiados cálculos o con cierta complejidad en su planteamiento (pensando en mis potenciales alumnos de Secundaria o Bachillerato)
Siempre me ha gustado, y como profesor me parece muy apropiado y didáctico, el analizar un problema desde distintos puntos de vista (usando distintas ideas, estrategias, procedimientos, ...) Pero me apasiona la búsqueda de un procedimiento simple con el que se puede resolver un problema matemático. La simplicidad en la resolución de los problemas es parte de la belleza que tienen las Matemáticas, y en este caso creo que encontré la idea simple que da con la solución a la pregunta en cuestión: la regla del producto...sí, aquella que dice que si tenemos 3 camisas y 5 pantalones distintos podemos vestirnos de 3.5=15 formas diferentes. Me explico:
El sorteo de emparejamientos realizado por la UEFA para emparejar a los equipos en los cuartos de final de la Liga de Campeones se puede equiparar a ordenar los 8 equipos, previamente numerados del 1 al 8, de forma que los dos primeros conformarían un emparejamiento, los dos siguientes otro, etc. En este caso habría 8.7.6.5.4.3.2.1=8! formas de hacerlo (usando la regla del producto, hay 8 equipos a escoger la primera vez, 7 la segunda, 6 la tercera, etc.)
 |
| Ejemplo de ordenación de los ocho equipos |
Es interesante hacer notar que cualquiera ordenación anterior es equiprobable, aspecto importante porque para calcular la probabilidad pedida sólo se va a utilizar la regla de Laplace.
Por otro lado, vamos a contabilizar las ordenaciones que permitirían un emparejamiento de equipos españoles: para ello imaginemos los ocho equipos ordenados y los separamos en bloques de 2 equipos (cada bloque conformaría un emparejamiento de cuartos de final)
 |
| 2-7, 5-4, 1-3 y 6-8 serían los emparejamientos de cuartos de final |
Tenemos que contabilizar las ordenaciones en las que hay dos equipos españoles en alguno de los cuatro bloques que conformarían un emparejamiento en cuartos. Fácil de calcular ya que:
- Hay 6 formas de elegir dos equipos españoles de entre los tres que hay (puedo elegir cualquier de los 3, luego cualquiera de los 2 que queda y usamos la regla del producto)
- Hay cuatro bloques donde elegir para ubicar a cualquiera de los 6 posibles emparejamientos de equipos españoles.
- Una vez ocupado un bloque con un emparejamiento de equipos españoles hay que ordenar los 6 equipos restantes y eso se hace de 6!=6.5.4.3.2.1 formas (la regla del producto de nuevo)
De nuevo, usando otra vez la regla del producto, tendremos 6.4.6! formas de ordenar los ocho equipos con un emparejamiento de equipos españoles.
Ya podemos terminar calculando la probabilidad de que haya un emparejamiento de equipos españoles en cuartos de final, siendo ésta:
Lógicamente, la probabilidad de que no haya emparejamiento español sería 4/7, con lo que es un "poco" más probable que no haya emparejamiento de equipos españoles.
PD: Cuando terminé de resolver el problema ya se había celebrado el sorteo y resultó que sí va a ver emparejamiento de equipos españoles (Barcelona- Atlético de Madrid).