Ayer surgió un "problema" en clase cuyo enunciado es:
Un
automóvil sube las cuestas a 54 Km/h, las baja a 90 Km/h y en llano marcha a 80
Km/h. Para ir de A a B tarda 2 horas y 30 minutos, y para volver de B a A, 2
horas y 38 minutos. ¿Cuál es la longitud del camino llano entre A y B si se
sabe que A y B distan 192 kilómetros?
Vamos a comenzar a pensar...
Fase 1: Entender el
enunciado
Vamos
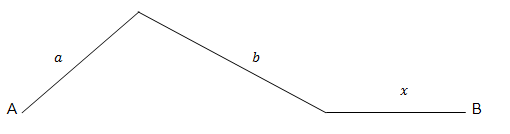
a suponer que primero hay un ascenso, luego un descenso y el trayecto final es
llano. También es necesario suponer que la velocidad, en cada tramo, es
constante (es decir, consideramos que el movimiento es rectilíneo uniforme)
Las
anteriores afirmaciones deberían haber estado en el enunciado, ya que una de
las cualidades que debe tener el enunciado de un problema es que sea claro y
sin ambigüedades.
Datos:
Velocidad
en ascenso= 54 km/h
Velocidad
en descenso= 90 km/h
Velocidad
en llano= 80 km/h
Tiempo
en ir desde A hasta B= 2 h 30 m=2,5 horas
Tiempo
en ir desde B hasta A= 2 h 38 min≈2,63 horas
Distancia
entre A y B=192 km
Fase 2: Buscar
relaciones
Obtenemos
un sistema de ecuaciones lineales (3 ecuaciones y 3 incógnitas, aunque a
nosotros sólo nos interesa una)
Fase 3: Resolver
Si
usamos, entre otros, Wiris (programa
de cálculo matemático) obtenemos:
Fase 4: Interpretar
(Además
hemos obtenido la longitud de los otros tramos)
Enlace a Wiris on line en
Andalucía:



No hay comentarios:
Publicar un comentario